| Soru 1: | |||||
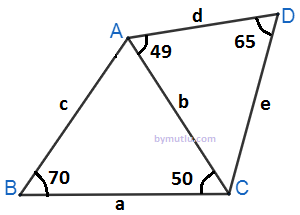
Şekildeki üçgende verilenlere göre en uzun kenar hangisidir?
|
|||||
Çözüm : ABC üçgeninde A köşesindeki iç açısı , 180 - ( 70 + 50 ) = 60 derece bulunur. Üçgende açı kenar bağıntısı kuralına göre , en büyük açının karşısında en uzun kenar vardır. Buna göre iç açıları küçükten büyüge sıraladığımızda, 50 < 60 < 70 olur, karşılarındaki kenarlarda aynı şekilde, c < a < b olarak yazılır. ADC üçgeninde C iç açısı da , 180 - ( 65 + 49 ) = 180 - 114 = 66 derece. Açılar küçükten büyüğe 49 < 65 < 66 olur. Karşılarındaki kenarlar da, e < b < d olur. ABC üçgeninde ki sıralama ile ADC üçgenindeki sıralamalar incelendiğinde, c < a < b için en uzun b oluyor ve, e < b < d için ise b den daha uzun d olmaktadır. Cevap : D |
|||||
| Soru 2: | |||||
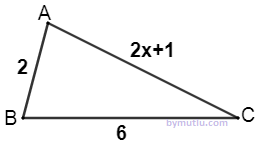
Şekildeki üçgende verilenlere göre x kaç tane tam sayı değeri alabilir?
|
|||||
Çözüm : Üçgen eşitsizliği kuralına göre, Bir üçgende herhangi bir kenarın uzunluğu , diğer iki kenarın toplamından küçük, ve farkından ise büyük olmalıdır. Bu özelliğe göre , 6 - 2 < 2 x + 1 < 6 + 2 4 < 2x + 1 < 8 4 - 1 < 2x < 8 - 1 3 < 2x < 7 3/ 2 < x < 7 / 2 1,5 < x < 3,5 x sayısı 1,5 ile 3,5 arasındaki tam sayılar olabilir. x = 2 ve x = 3 olabilir , 2 tane tam sayı vardır. Cevap : B |
|||||
| Soru 3 : | |||||
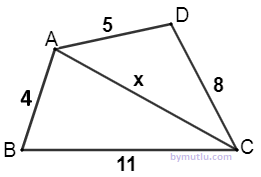
Şekildeki üçgende verilenlere göre x uzunluğunun alabileceği tam sayı değeri en çok kaçtır?
|
|||||
Çözüm : ABC ügeninde Üçgen eşitsizliği kuralına göre, 11 - 4 < x < 11 + 4 7 < x < 15 olur. Buna 1. durum diyelim. ADC üçgeninde verilenlere göre x in değer aralığı , 8 - 5 < x < 8 + 5 3 < x < 13 olur. Buna da 2. durum diyelim. Şimdi x in alabileceği tam sayı değerleri , 1. durum ve 2. durumun ortak elemanları olmalıdır. 1 . durum da x yerine 8,910,11,12,13,14 olabilir. 2. durumda x yerine 4,5,6,7,8,9,10,11,12 olabilir. her ikisinde ortak olan tam sayı değerleri, 8 , 9 , 10 , 11 ,12 olup x en çok 12 olabilir. Cevap : D |
|||||