açıklamalı olarak anlatıldığı , lise yazılı sınavlarda , tyt yks ayt, açık öğretim lisesi gibi sınavlarda
faydalı olacak bir sayfadır. 16 tane soru ve daha fazlası.
İKİNCİ DERECEDEN DENKLEMLER
1) x2-9=0 denkleminin çözüm kümesi nedir?
|
Çözüm : x2-9=0 ise x2=9 karesi 9 a eşit olan -3 ve 3 olur. |
||||||||||||||||||||||||||||||||
2) (x-5)(x+3)=0 ise çözüm kümesi hangisidir?
|
Çözüm: (x-5) . (x+3)=0 ise çarpanlar ayrı ayrı 0' a eşitlenip x in değerleri bulunur. x-5=0 ise x+3=0 ise x=5 x=-3 |
||||||||||||||||||||||||||||||||
3) x2 - 4x=0 denkleminin çözüm kümesi nedir?
|
Çözüm: x2 - 4x=0 ise çarpanlara ayıralım. x.(x-4)=0 olup ayrı ayrı 0'a eşitlenir. x=0 ve x-4=0 x=4 o halde Ç={0,4} |
||||||||||||||||||||||||||||||||
4) x2 - 5 x + 6 = 0 denkleminin çözüm kümesi nedir?
|
Çözüm: x2 - 5 x + 6 = 0 ise çarpanlara ayıralım Çarpımları +6 ve toplamları -5 olan iki sayı (-2) ve (-3) olup, verilen ifade (x-2).(x-3)=0 olarak yazılır. x-2=0 ise x=2 , ve x-3=0 ise x=3 olur. Ç= {2,3} olur.
|
||||||||||||||||||||||||||||||||
5) x2 + 16 = 0 ise çözüm kümesi nedir?
|
Çözüm: x2 + 16 = 0 ise x2 = -16 Karesi alındığında -16 yı veren bir reel sayı yoktur . Bu yüzden bu denklemi sağlayan reel sayı kök yoktur. Ç= { } olur. Boş küme.
|
||||||||||||||||||||||||||||||||
6) x2 - m x - 12 =0 denkleminin köklerinden biri 2 olduğuna göre m kaçtır?
|
Çözüm : 2 bu denklemin kökü ise denklemi sağlar. x in yerine denklemde 2 yazalım. 22 - m .2 - 12 = 0 ise 4-2m-12=0 -8-2m=0 -2m=8 ise her iki taraf -2 ile bölünürse m=8/-2 m=-4 |
||||||||||||||||||||||||||||||||
7) x2 + m x - 18 =0 denkleminin köklerinden biri 9 ise diğer kökü nedir?
|
Çözüm: 9 bu denklemi sağlar. x in yerine 9 yazılıp m bulunur. 92 + m 9 - 18 =0 81+9m -18 =0 9m+63 =0 ise 9m=-63 , m=-63/9 ise m=-7 olur. denklem ; x2 -7x - 18 =0 olup, çarpanlara ayrılabilir. Çarpımları -18 ve toplamları -7 olan iki sayı (-9) ve (+2) dir. (x-9).(x+2)=0 yazılır. buradan x-9=0 ise x=9 , diğer kök x+2=0 ise x=-2 bulunur. |
||||||||||||||||||||||||||||||||
8) x2 - 2 x + m - 4 =0 denkleminin eşit iki gerçel kökü varsa m kaçtır?
|
Çözüm: Δ= b2 - 4 . a.c = 0 olmalıdır. (-2)2 - 4 . 1.(m-4)=0 4- 4m+16 =0 -4m + 20 =0 -4m =-20 m = -20/-4 m = 5
|
||||||||||||||||||||||||||||||||
9) 3x2 - x + m - 1 =0 denkleminin farklı iki reel kökünün olması için m ne olmalıdır ?
|
Çözüm: Δ= b2 - 4 . a.c > 0 olmalıdır. (-1)2 - 4 . 3.(m-1) > 0 1- 12 m + 12 > 0 -12 m + 13 > 0 -12 m > -13 m < -13 /-12 ( Eşitliğin her iki tarafı negatif -12 ye bölününce büyük işareti küçük işareti olarak değişir.) m < 13 /12
|
||||||||||||||||||||||||||||||||
10) Kökleri 3 ve 7 olan ikinci dereceden denklemi yazınız.
|
Çözüm: x1 = 3 ve x2= 7 ise T = x1 + x2 ve Ç = x1 . x2 olmak üzere , T = 3 + 7 = 10 ve Ç = 3. 7 = 21 Genel denklem ; x2 -T x + Ç =0 x2 -10 x + 21 =0 olur. |
||||||||||||||||||||||||||||||||
11) Kökleri -8 ve 5 olan ikinci dereceden denklem nedir?
|
Çözüm: x1 = - 8 ve x2 = 5 ise T = x1 + x2 ve Ç = x1 . x2 olmak üzere , T = - 8 + 5 = - 3 ve Ç = ( - 8 ) . 5 = - 40 Genel denklem ; x2 -T x + Ç =0 x2 - ( - 3 ) x + ( - 40 ) = 0 x2 + 3 . x - 40 = 0 olur. |
||||||||||||||||||||||||||||||||
12) x2 - 2x - 6 = 0 Denkleminin kökleri x1 ve x2 olduğuna göre ; x1 + x2 = ? x1 . x2 = ?
|
Çözüm: a = 1 , b = -2 , c = -6
|
||||||||||||||||||||||||||||||||
13) x2 - 7x + 3 = 0 Denkleminin kökleri x1 ve x2 olduğuna göre ;
|
Çözüm: a = 1 , b = -7 , c = 3
|
||||||||||||||||||||||||||||||||
14 ) 3 x2 - m x + 5 = 0 Denkleminin kökleri x1 ve x2 dir. x1 + x2= 4 olduğuna göre m kaçtır?
|
Çözüm: a = 3 , b = -m , c = 5
ise m = 3 . 4 = 12 |
||||||||||||||||||||||||||||||||
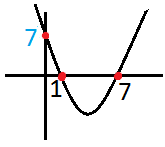
15) x2 - 8 x + 7 = 0 denklemi verilen parabol x eksenini hangi noktalarda keser ?
|
Çözüm: Denklemin kökleri x1 ve x2 parabolün x eksenini kestiği noktaları verir. x2 - 8 x + 7 = 0 ise çarpanlara ayıralım Çarpımları +7 ve toplamları -8 olan iki sayı (-1) ve (-7) olup, verilen ifade (x-1).(x-7)=0 olarak yazılır. x-1=0 ise x=1 , ve x-7=0 ise x=7 olur. Ç= {1,7} olur. |
||||||||||||||||||||||||||||||||
16)
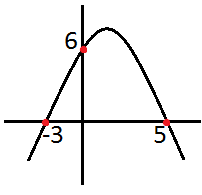
Şekilde grafiği verilen parabolün denklemi nedir?
|
Çözüm: Denklemin kökleri x1 ve x2 parabolün x eksenini kestiği noktalardır. Genel denklem y = a . ( x - x1 ) . ( x - x2 ) olup, a yı bulmak için, Parabolün y eksenini kestiği nokta ( 0 , 6 ) bu denklemi sağlar. y = a . ( x - (-3) ) . ( x - 5 ) 6 = a . ( 0 + 3 ) . ( 0 - 5 ) 6 = -15 . a a = 6 / -15 a = - 2 / 5 Denklem , y = -2/5 .( x + 3 ) . ( x - 5 ) y = -2 .( x2 - 2 x - 15 ) / 5 |
||||||||||||||||||||||||||||||||