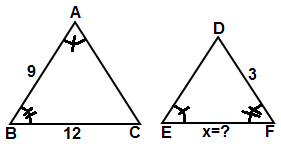
1) Şekildeki üçgenlerde verilenlere göre | EF | = x uzunluğu kaçtır? |
Çözüm: İki üçgenin iki iç açısı eşit olunca , üçüncü iç açılarda eşit olur. m ( C ) = m ( D ) olur. Eşit açılara göre sıra ile yazalım. ABC = EFD üçgenlerinde Açı Açı Açı benzerliği olup , eşit açıların karşısındaki kenar uzunlukları oranı eşittir. Eşit açıların karşısındaki kenarları oranlayıp , bilinmeyeni bulmalıyız. 12 / 3 = 9 / x ise içler dışlar çarpımından 12 x = 27 x = 27 / 12 sadeleşirse, x = 9 / 4 Cevap : 9 / 4 |
|
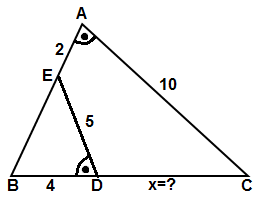
2) Şekildeki üçgende verilenlere göre x kaçtır?
|
Çözüm: Şekilde iki tane üçgen görülüyor. Bu iki üçgenin A ve D açıları eşit , B açısıda ortak açıdır. O halde E ile C açıları da eşit olacağından, sıra ile yazarsak , ABC = DBE olarak benzerdir denir. Benzer iseler karşılıklı kenarların oranı eşittir. 5 / 10 = 4 / ( 2 + | BE | ) eşitliğinden 2 + | BE | = 8 olur . | BE | = 6 Ayrıca , 5 / 10 = | BE | / ( 4 + x ) 5 / 10 = 6 / ( 4 + x ) 5 in 2 katı 10 ise 6 nın 2 katı 12 olur. 4 + x = 12 x = 8 bulunur. Cevap : 8 |
|
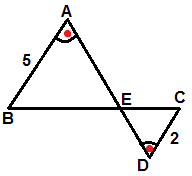
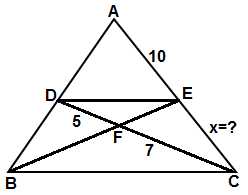
3) Şekilde | AD | = 28 ise verilenlere göre , | ED | = x kaçtır ?
|
Çözüm: A ve D içters açılar ise AB // CD olur. ABE ve DCE üçgenleri benzerdir , çünkü açılar sıra ile eşittir .( A =D , B = C , E = E ) Açı Açı Açı benzerliğinden karşılıklı kanarlar orantılıdır. | ED | = x ise | AE | = 28 -x 2 / 5 = x / (28 - x ) eşitliğinden x = 8 bulunur. Yada Kelebek benzerliği olarak düşünürsek , 7 k = 28 ise k = 4 | ED | = x = 2k = 2 . 4 = 8 Cevap : 8 |
|
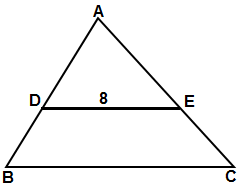
4) Şekildeki üçgende | AD | / | DB | = 4 / 3 ise verilenlere göre , | BC | kaçtır? |
Çözüm: Cevap : 14 |
|
5 ) Şekildeki üçgende verilenlere göre | EC |=x kaçtır?
|
Çözüm: Cevap : 4 |
|
| Devamı .. | |||
| Üçgende Benzerlik Çözümlü Sorular 1 | Üçgende Benzerlik Çözümlü Sorular 2 | Üçgende Benzerlik Çözümlü Sorular 3 | |