Geometri dersinin en önemli konularından biri olan ,
10. sınıf dörtgenler ve özellikleri ile ilgili çözümlü soru örnekleri aşağıdadır.
10. sınıf matematik dersi konularından dörtgenlerden, Üniversite giriş Lisans yerleştirme sınavlarında
dörtgenler ile ilgili en az 3 adet soru gelmektedir.
Dörtgenler konusu ile ilgili soruları çözebilmeniz için dörtgenlerin özelliklerini ,
dörtgende açı özellikleri, kenarlar ve köşegenler ile ilgili özellikler , dörtgende alan ile ilgili özellikler
ve bazı kuralların çok iyi bilinmesi gereklidir.
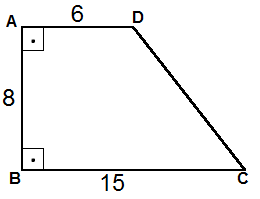
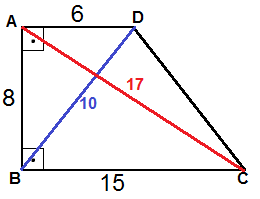
1)
Şekildeki dörtgende verilenlere göre, ABCD dörtgeninin köşegen uzunluklarının toplamı kaçtır?
|
Çözüm :
Köşegenler çizilince oluşan dik üçgenlerde, pisagor teoreminden , ABD üçgeninde BD uzunluğu 6 - 8 - 10 üçgeninde, | BD | = 10 olur. ABC üçgeninde AC uzunluğu 8 - 15 - 17 üçgeni , | AC | = 17 olur . Köşegen uzunlukları toplamı 10 + 17 = 27 olur. |
|||||||||
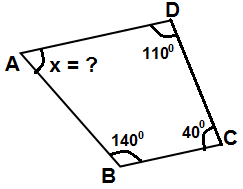
2 )
Şekildeki dörtgende verilenlere göre, m ( BAD ) = x açısı kaç derecedir?
|
Çözüm : Dörtgende iç açıların ölçüleri toplamı 360 derecedir. Buna göre ; x + 140 + 40 + 110 = 360 x + 290 = 360 x = 360 - 290 x = 70 |
|||||||||
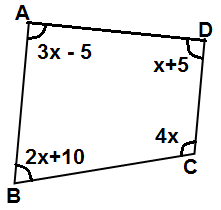
3)
Şekildeki dörtgende verilenlere göre, x kaç derecedir?
|
Çözüm : Dörtgende iç açıların ölçüleri toplamı 360 derecedir. Buna göre ; 3x - 5 + 2x + 10 + 4x + x + 5 = 360 10x + 10 = 360 10 x = 360 - 10 10 x = 350 x = 350 / 10 x = 35 derece. |
|||||||||
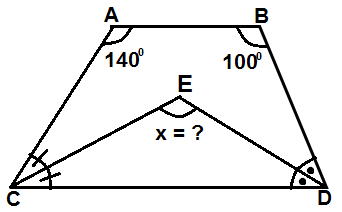
4 )
Şekildeki dörtgende verilenlere göre , x açısı kaç derecedir ?
|
Çözüm : 1.yol : Açıortaylara sırasıyla a , a ve b , b diyelim . Dörtgende iç açılar toplamı 360 derecedir. a + a + b + b + 140 + 100 = 360 2 a + 2 b = 360 - 240 2 . ( a + b ) = 120 a + b = 120 / 2 a + b = 60 ise , CEB üçgeninde iç açılar toplamı 180 olacağından, x + a + b = 180 x + 60 = 180 x = 180 - 60 x = 120 2. yol : Dörtgende birbirine komşu olan iki iç açıortayın , kesim noktasında oluşan açı , diğer iki iç açının toplamının yarısına eşittir. x = ( 140 + 100 ) / 2 x = 240 / 2 x = 120 |
|||||||||
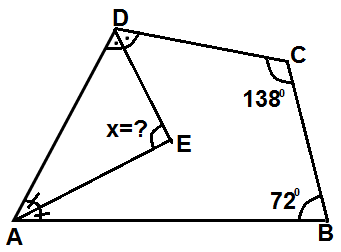
5)
Şekildeki dörtgende verilenlere göre, x açısı kaç derecedir?
|
Çözüm : x = ( 138 + 72 ) / 2 x = 210 / 2 x = 105
|
|||||||||
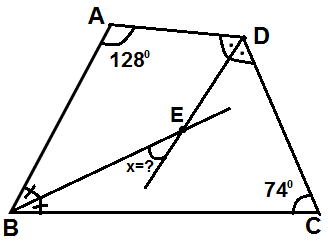
6 )
Şekildeki dörtgende verilenlere göre, x kaç derecedir?
|
Çözüm : Dörtgende özellik ; Birbirine komşu olmayan iki iç açının , açıortaylarının kesim noktasındaki açının ölçüsü, Diğer iki iç açının farkının , mutlak değerinin yarısına eşit olur. Buna göre ; x = ( 128 - 74 ) / 2 x = 54 / 2 x = 27 |
|||||||||
|
||||||||||
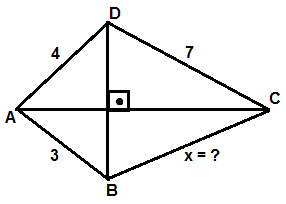
7 )
Şekildeki dörtgende verilenlere göre, | BC | = x uzunluğu kaçtır ?
|
Çözüm : Dörtgende köşegenler birbirini dik keserse, karşılıklı kenarların kareleri toplamı eşittir. 4 2 + x 2 = 3 2 + 7 2 16 + x 2 = 9 + 49 x 2 = 58 - 16 x 2 = 42 x = √42 |
|||||||||
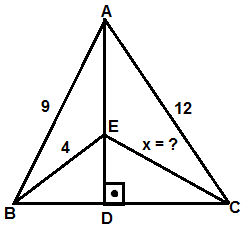
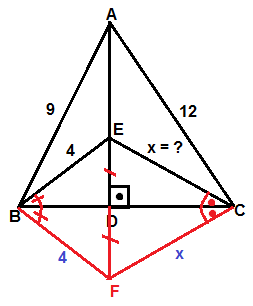
8 )
Şekildeki dörtgende verilenlere göre, | BC | = x uzunluğu kaçtır ?
|
Çözüm :
BEC üçgeninin simetriği çizildiğinde oluşan dörtgende köşegenler diktir. 9 2 + x 2 = 4 2 + 12 2 81 + x 2 = 16 + 144 x 2 = 160 - 81 x 2 = 79 x = √79 |
|||||||||
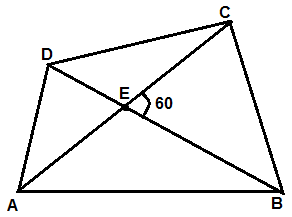
9)
ABCD bir dörtgen . m ( BEC ) = 60 , | AC | = 14 ve | BD | = 6 ise A ( ABCD ) = ?
|
Çözüm : Verilen dörtgenin alanı özellik yardımıyla , A ( ABCD ) = 1/2 . | AC | . | BD | . Sin 60
A ( ABCD ) = 21 √3 |
|||||||||
10)
Şekilde ABCD dörtgeninde verlilenlere göre , A ( AEB ) = ? |
Çözüm : Dörtgende özellik ten , 8 . x = 6 . 10 olur . x = 60 / 8 x = 15 / 2 = 7 , 5 birim kare |
|||||||||
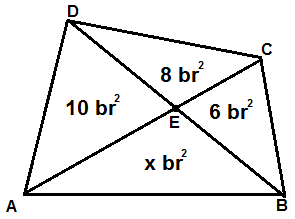
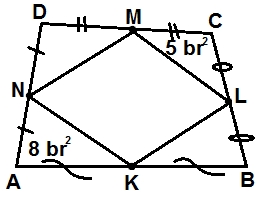
11)
Şekildeki ABCD dörtgeninde verilenlere göre , dörtgenin alanı A ( ABCD ) nedir?
|
Çözüm : KLMN kenarların orta noktaları ise, Dörtgenlerde özellik gereği , 8 + 5 = A (NDM) + A ( KBL ) = 13 olur. 4 küçük üçgenin alanının toplamı A (KLMN) olur. A (KLMN) = 8 + 5 + A (NDM) + A ( KBL ) A (KLMN) = 13 + 13 = 26 Ayrıca, A ( KLMN) = A ( ABCD ) / 2 dir. Buradan , A ( ABCD ) = 2 . A ( KLMN) = 2. 26 2 . 26 = 52 olur. |
|||||||||