İkinci dereceden fonksiyonlar grafikleri parabol soruları ygs lys sınavları için örnek soru çözümleri anlatılmaktadır.
| Parabol Çizimi Soruları : | ||
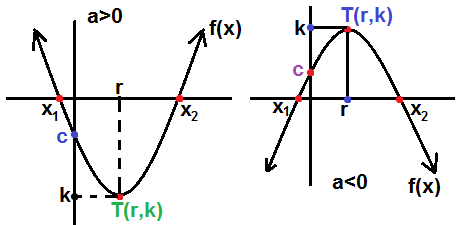
İkinci dereceden fonksiyonun grafiğini Çizmek için : y = f ( x ) = a x 2 + b x + c 1 ) a > 0 ise parabolün kolları yukarı doğru olur. a < 0 ise parabolün kolları aşağı doğru olur . 2 ) x = 0 için y eksenini kesen nokta bulunur. Genelde ( 0 , c ) noktasıdır . 3 ) y = f ( x ) = 0 için , denklemin kökleri bulunur. Bu kökler parabolün x eksenini kestiği noktalardır . Parabol x eksenini ( x 1 , 0 ) ve ( x 2 , 0 ) noktalarında keser . ( Eğer Delta >0 , reel kök varsa ) Eğer Delta = 0 ise x eksenine teğet , yani tek noktada keser. x 1 = x 2 Eğer Delta < 0 ise parabol x eksenini kesmez. 4 ) Parabolün tepe noktasının koordinatları T ( r , k ) bulunur. r = - b / 2a yada r = ( x 1 + x 2 ) / 2 k = ( 4 a c - b 2 ) / 4.a formülü yada , k = f ( r ) ile ( fonksiyonda x in yerine r yazılır.) Bulunan bu değerlere göre Grafik şöyle olur. |
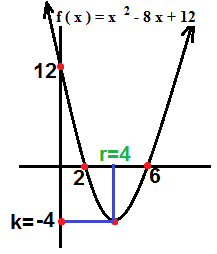
Örnek : y = f ( x ) = x 2 - 8 x + 12 fonksiyonunun grafiğini çiziniz. Çözüm : a = 1 , b = - 8 , c = 12 a > 0 olup kolları yukarı doğru olacak. x = 0 için y = 12 olup , y yi ( 0 , 12 ) de keser. y = 0 için denklemin kökleri ; x 2 - 8 x + 12 = 0 çarpanlara ayırarak bulalım. ( x - 2 ) . ( x - 6 ) = 0 ise x 1 = 2 ve x 2 = 6 dir. Tepe noktasını T ( r , k ) r = ( x 1 + x 2 ) / 2 = ( 2 + 6 ) / 2 = 4 k = f ( r ) = f ( 4 ) = 4 2 - 8 . 4 + 12 = 16 - 32 + 12 = - 4 olur. Grafik çizimi ise , bulunan noktaları koordinat düzleminde tespit edip birleştiriyoruz.
|
|
|
||