Küme tanımı, elemanları , alt küme , kümelerde kesişim birleşim fark işlemleri ve kümelerle ilgili problem çözümleri açıklamalı olarak anlatılıyor.
KÜMELER
1) A = { 1 , 2 , { 3 , 4 },5 , 6 } ise, A kümesinin eleman sayısı kaçtır?
|
Çözüm : { 3 , 4 } tek eleman olarak sayılacaktır , bu durumda A kümesinin eleman sayısı 5 tane S( A ) = 5 olur.
|
|
2) A = { x | , -3 < x < 5 , x ∈ Z } ise A kümesinin elemanları hangileridir?
|
Çözüm:
|
|
3) A = { x | , -3 < x < 5 , x ∈ N } ise A kümesinin elemanları hangileridir?
|
Çözüm: x ∈ N , yani kümenin elemanları -3 ile 5 arasındaki doğal sayılar olur. A = { 0 , 1 , 2 , 3 , 4 } olur . S ( A ) = 5 elemanlıdır. |
|
4) A = { a , b , c } kümesinin alt kümelerini yazınız , alt küme sayısı kaçtır ?
|
Çözüm: Sıfır elemanlı alt küme : { } , 1 tane Bir elemanlı alt kümeler : { a } , { b } , { c } 3 tane İki elemanlı alt kümeler : { a , b } , { a , c } , { b , c } 3 tane Üç elemanlı alt kümeler : { a , b , c } 1 tane Alt küme sayısı toplamı : 1 + 3 + 3 + 1 = 8 tane olur. Ayrıca , Alt küme sayısı = 2 n = 2 3 = 2 . 2 . 2 = 8 olur.
|
|
5) A = { a , b , c , d , e , f } kümesinin alt küme sayısı ve öz alt küme sayısı kaçtır ?
|
Çözüm: S ( A ) = 6 ise n = 6 alınır. Alt küme sayısı = 2 n = 2 6 = 2 . 2 . 2 . 2 . 2 . 2 = 64 olur. Özalt küme sayısı = 2 n - 1 = 64 - 1 = 63 olur. |
|
6) 32 tane alt kümesi olan bir kümenin eleman sayısı kaçtır?
|
Çözüm : 2 n = 32 ise n sayısı kümenin eleman sayısıdır. Kaç tane 2 nin çarpımı 32 olur diye düşünürüz. 32 : 2 = 16 , 16 : 2 = 8 , 8 : 2 = 4 , 4 : 2 = 2 , 2 : 2 =1 olup, 5 kez 2 ye bölme işlemi uygulandı . n = 5 olur. küme 5 elemanlıdır. |
|
7 ) 127 tane öz alt kümesi olan bir küme kaç elemanlıdır?
|
Çözüm : 2 n -1 = 127 2 n = 127+ 1 2 n = 128 , ise n sayısı kümenin eleman sayısıdır. Kaç tane 2 nin çarpımı 128 olur diye düşünürüz. 128: 2 = 64 , 64 / 2 = 32 , 32 : 2 = 16 , 16 : 2 = 8 , 8 : 2 = 4 , 4 : 2 = 2 , 2 : 2 =1 olup, 7 kez 2 ye bölme işlemi uygulandı . n = 7 olur. küme 7 elemanlıdır. |
|
8 ) A = { a , b , c , d , e } kümesinin alt kümelerinin kaç tanesinde "b" eleman olarak bulunmaz ?
|
Çözüm : Bu gibi sorularda verilen eleman hariç tutulup , geriye kalan elemanlardan oluşan yeni kümenin alt küme sayısı cevap olur. b hariç , { a , c , d , e } kümesinden oluşan alt kümeler aynı zamanda A kümesininde içinde "b" olmayan alt kümeleri olmaktadır . O halde , cevap 2 4 = 16 tanesinde b olmaz. |
|
9 ) A = { a , b , c , d , e } kümesinin alt kümelerinin kaç tanesinde "b" eleman olarak bulunur ?
|
Çözüm : Bütün alt kümeler - İçinde "b" olmayan alt kümeler cevap: 2 5 - 2 4 = 32 - 16 = 16 tanesinde de b bulunur. |
|
10 ) A = { a , b , c , d , e } kümesinin alt kümelerinin kaç tanesinde a veya c eleman olarak bulunur ?
|
Çözüm : Bütün alt kümeler - İçinde a ve c ( ikisi aynı anda bulunmayan ) alt kümeler cevap: 2 5 - 2 3 = 32 - 8 = 24 tanesinde a veya c den biri mutlaka vardır. |
|
11 ) A = { a , b , c , d , e } kümesinin alt kümelerinin kaç tanesinde a ve c eleman olarak bulunur ?
|
Çözüm : a ve c bulunur demek ikisi aynı anda kesin var demek . a ile c hariç {b , d , e } kümesinden oluşan alt kümeler 2 3 = 2.2.2 = 8 tanedir , Şimdi bu 8 tane kümenin içine a ve c yi de biz eklediğimizi düşündüğümüzde , o zaman içinde a ve c nin kesin bulunduğu alt kümelerin de 8 tane olduğu anlaşılacaktır. cevap 8 dir. |
|
12 ) A = { a , b , c , d , e } kümesinin alt kümelerinin kaç tanesinde a bulunup b eleman olarak bulunmaz ?
|
Çözüm : a ve b yi ilk önce saymayız , oluşan alt kümelere a yı sonradan yazdığımızı düşünüyoruz. a ile b hariç {c , d , e } kümesinden oluşan alt kümeler 2 3 = 2.2.2 = 8 tanedir , Şimdi bu 8 tane kümenin içine "a" yı eklediğimizi düşündüğümüzde , o zaman içinde a nıın olduğu b nin olmadığı alt kümeler oluşur , 8 tane olduğu anlaşılacaktır. cevap 8 dir. |
|
13 ) A={a, b , 1, ,2, 4 } B={a, c , 1 , 3 , 5 , 7 } kümeleri veriliyor. Birleşim ve kesişim kümelerini yazınız.
|
Çözüm : Kesişim kümesine , her iki kümede de olan ortak elemanlar yazılır. A ∩ B = {a, 1 } Birleşim kümesine ise her iki kümedeki bütün elemanlar yazılır , ancak bir eleman iki kez yazılmaz bir kez yazılır. A ∪ B = {a, b , c , 1 , 2 , 3 , 5 , 7 } |
|
14) A ∩ B ≠{ } S ( A ) = 2 . S ( B ) 2 .S ( A \ B) = 5. S ( B \ A ) olduğuna göre , B kümesi en az kaç elemanlıdır?
|
Çözüm : S ( A \ B) = 5x , S ( B \ A ) = 2x diyelim. S ( A ∩ B ) = c olsun. S ( A ) = 5x + c ve S ( B ) = 2 . x + c olur. S ( A ) = 2 . S ( B ) ise , 5x + c = 2 . ( 2 . x + c ) 5x + c = 4x + 2 c 5x - 4x = 2c -c x = c olur . Bu durumda S ( B ) = 2 x + c = 2 c + c = 3.c olup, c = 1 için en az S( B ) = 3 elemanlı olur. |
|
15 ) Herkesin en az bir oyun oynadığı 30 kişilik bir sınıfta , Futbol oynayan 20 , Basketbol oynayan 16 kişi ise , her iki oyunu da oynayan kaç kişi vardır?
|
Çözüm : S ( F ) = 20 , S ( B ) = 16 , S ( F ∪ B ) = 30 , S ( F ∩ B ) = ? Formül den ; S ( F ∪ B ) = S ( F ) + S ( B ) - S ( F ∩ B ) 30 = 20 + 16 - S ( F ∩ B ) S ( F ∩ B ) = 36 - 30 S ( F ∩ B ) = 6 kişi vardır. |
|
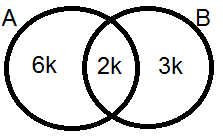
16) S ( A -B ) = 2 . S( B - A) = 3 S (A ∩ B ) ve S ( A ) - S ( B ) = 6 olduğuna göre S ( A ∪ B ) =?
|
Çözüm : Bu tür sorularda kat sayıların ekok u alınır . Ekok ( 1, 2, 3 ) = 6 olur. Buradan S ( A -B ) = 6k , S( B - A) = 3k ve S (A ∩ B )= 2k denir. Şekil üzerine verilenleri yazalım .
S ( A ) = 6k + 2k = 8k , S ( B ) = 3k + 2k = 5k S ( A ) - S ( B ) = 6 ise 8k - 5k =6 , 3 k = 6 ise k=6/3 , k=2 olur. S ( A ∪ B ) = 6k + 2k + 3k = 11 k = 11 . 2 = 22 olur. |
|
| KÜMELER BULUNUR BULUNMAZ SORULARI | ||
17) A = { 1 , 2 , 3 , 4 , 5 , 6 , 7 } kümesinin 3 elemanlı alt kümelerinin kaç tanesinde 4 bulunur ?
|
Çözüm : Bu tür sorularda 7 elemanlı bir kümenin 3 elemanlı alt küme sayısı C ( 7 , 3 ) = 35 ( 7 nin 3 lü kombinasyonu ) 35 tane 3 elemanlı alt küme var demektir . Ancak bunların bazılarında 4 vardır , bazılarında yoktur . Şimdi 4 ü ayrı tutup , 4 ün olmadığı 3 elemanlı alt kümeleri oluşturacak olursak , Geriye 6 eleman kalacaktır . C ( 6 , 3 ) = 20 olup bunlarda 4 elemanı bulunmaz. O halde Bütün 3 elemanlı alt kümelerden , İçinde 4 ün bulunmadığı 3 elemanlı alt kümeleri çıkarırsak, geriye içinde 4 bulunan 3 elemanlı alt kümeler kalır. Cevap : C ( 7 , 3 ) - C ( 6 , 3 ) = 35 - 20 = 15 olur. 2. YOL : 4 hariç geriye A = { 1 , 2 , 3 , 5 , 6 , 7 } 6 eleman kalır . Bu 6 elemandan oluşan 2 elemanlı alt kümeler C ( 6 , 2 ) = 6.5 / 2.1 = 15 tanedir . İşte bu 15 tane kümenin içine 4 ü eleman olarak eklediğimizde oluşan kümeler hem 3 elemanlı hemde içinde 4 ün bulunduğu kümeler olur. 15 tanedir bunlar.
|
|
18) A = { 1 , 2 , 3 , 4 , 5 , 6 , 7 } kümesinin 3 elemanlı alt kümelerinin kaç tanesinde 4 bulunur , 5 bulunmaz ?
|
Çözüm : 4 ve 5 hariç geriye 5 eleman kalır . İstenen alt kümeler 3 elemanlı olduğundan , bu 5 elemandan oluşan 2 elemanlı alt kümeleri yazıyoruz . Niye 2 elemanlı , çünkü daha sonra bunların içine bulunsun dediği 4 ü ekleyeceğiz. C ( 5 , 2 ) = 5.4 / 2 . 1 = 20 / 2 = 10 tanedir. Bu 10 tane kümede 4 ve 5 yoktur ve 2 elemanlıdırlar. Bunlara 4 ü yazarsak hem 3 elemanlı olurlar hemde içinde 4 vardır 5 yoktur. Cevap 10 dur. |
|
19 ) A = { a , b , c , d , e , f , g , h , k , l , m } kümesinin 4 elemanlı alt kümelerinin kaç tanesinde "a" ve "b" bulunup , "c" bulunmaz ?
|
Çözüm : Bu tip sorularda izlenecek yol şudur ; Normalde 11 elemanlı bu kümenin 4 elemanlı alt kümeleri ; C ( 11 , 4 ) kadardır . Soruda verilen 3 tane elemanı 11 den çıkarıyoruz. Sonra 4 elemandanda bulunması istenilen kadar eleman için yer açılacak , yani 4 tende 2 çıkacak ( a ve b için). O halde cevap C ( 11-3 , 4 - 2 ) = C ( 8 , 2 ) = 8 . 7 / 2 . 1 = 28 olur. |
|
20 ) A = { a , b , c , d , e , f , g , h , k , l , m , n , p , r } kümesinin 6 elemanlı alt kümelerinin kaç tanesinde b , c bulunup , k , m , n bulunmaz ?
|
Çözüm : C ( 14 , 6 ) düzenleme yapıyoruz . 14 ten 5 eleman çıkacak , ve 6 dan da 2 çıkacak ( bulunsun denilen kadar .) Cevap : C ( 14 -5 , 6 - 2 ) = C ( 9 , 4 ) = 9 .8.7.6 / 4.3.2.1 = 126 olur. |
|
21 ) A = { a , b , c , d , e , f , g , h , k , l , m , n , p , r } kümesinin 6 elemanlı alt kümelerinin kaç tanesinde b veya c bulunup , k , m , n bulunmaz ?
|
Çözüm : Bu soruda ise ; b , c , k , m , n elemanları dışında geriye 14 - 5= 9 eleman kalıyor . k , m , n bulunmayan bütün 6 elemanlı alt kümelerden , ( 11,6) b , c , k , m , n bulunmayan 6 elemanlı alt kümeler çıkarılınca (9,6) geriye içinde b veya c olan, fakat k , m , n elemanlarının olmadığı 6 elemanlı alt kümeler kalacaktır. Cevap : k , m , n hariç 14 - 3 = 11 eleman kalıyor. ( a ve b var .) C ( 11 , 6 ) - C ( 9 , 6 ) = 462 - 84 = 378 |
|
Devamı..
| KONU | KÜMELER | TEST |
| Alt küme soruları | KÜMELER ÇÖZÜMLÜ SORULAR1 | TEST1 |
| Kümelerde işlemler soruları | KÜMELER ÇÖZÜMLÜ SORULAR 2 | TEST2 |
| Küme problemleri soruları | KÜMELER ÇÖZÜMLÜ SORULAR 3 | |
| Küme problemleri soruları | ÇÖZÜMLÜ SORULAR 4 | |
| Küme problemi çözümü şekilli | ÇÖZÜMLÜ SORULAR 5 | |
| Küme Problemleri Soruları Şekilli Çözümler. | ÇÖZÜMLÜ SORULAR 6 |