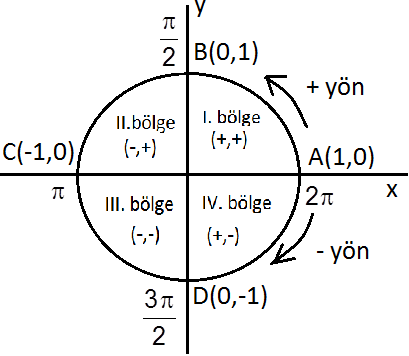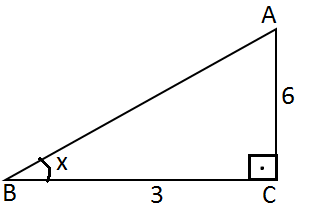Kategori: Trigonometri
Çarşamba, 03 Şubat 2016 tarihinde yayınlandı.
Trigonometri çözümlü sorular ve konu anlatımı lys
TRÄ°GONOMETRÄ° Â
BİRİM ÇEMBER :
Merkezinin koordinatları eksenlerin başlangıç noktası
ve yarı çapı 1 birim uzunlukta olan çembere
 trigonometri  çemberi veya birim çember denir.
Birim çemberin yarı çapı r=1  olduÄŸundan çevresiÂ
2 π  birimdir.
 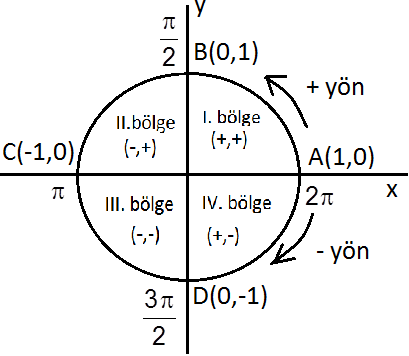 |
 |
|
Çemberin çevresi, 3600 derece , 2 π  radyan, yada 400 Grad a eşittir. Buna göre;
 D Â
180 |
= |
  R
  π |
= |
 G Â
200 |
eşitlikleri yazılır.
|
 |
 TRİGONOMETRİK FONKSİYONLAR
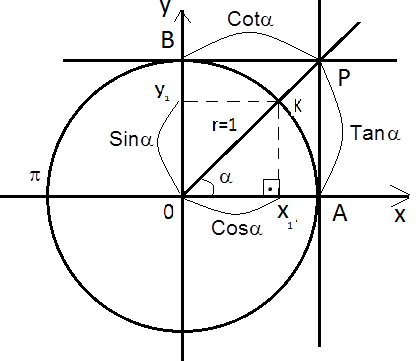
Trigonometrik çember üzerinde K(x1,y1)  olmak üzere,
 Sinα=y1 , Cosα=x1  ,  Tanα=|AT|,  Cotα=|BP|  olur.
 Sin2α+Cos2α=1  olur.  Buradan,
 Sin2α=1-Cos2α  ,   Cos2α=1-Sin2α   olur.
|
 |
 Dik  Üçgenlerde trigonometrik oranlarÂ
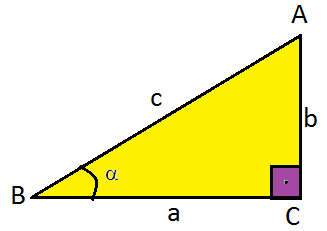
|
Â
Sinα=
|
 b
 c  |
Karşı dik kenar uzunluÄŸu Â
Hipotenüs uzunluğu |
|
Â
 Cosα=
|
  b
 c |
 KomÅŸu dik kenar uzunluÄŸu Â
Hipotenüs uzunluğu |
|
Â
tanα=
|
 b
 a  |
Karşı dik kenar uzunluÄŸu Â
Komşu dik kenar uzunluğu |
|
Â
Cotα=
|
 a
 b |
 KomÅŸu dik kenar uzunluÄŸu Â
Karşı dik kenar uzunluğu |
|
Â
Secα=
|
   1
  Cosα  |
  cÂ
  a |
|
Â
Cesecα=
|
   1
  Sinα |
  c Â
  b |
|
tanα=
|
 Sinα Â
 Cosα  |
 ise  tanα.Cotα=1  olur. |
|
 |
|  Secα.Cosα=1    ,  coseccα.Sinα=1 |
 |
|
 Şekilde  m(A)+m(B)=90   ise Â
SinA=CosB Â , Â SinB=CosA , Â tanA=CotB Â , Â cotA=tanB Â olur.
|
 |
|
 Örnek:
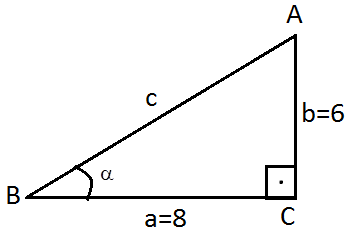
Şekildeki dik üçgende verilenlere göre Sinα=?  Cosα=?  tanα=?  Cotα=?
Çözüm:   Hipotenüs uzunluğu c=?  pisagor teoremi ile c bulunur.
c2=a2+b2   ise  c2=82+62  ,   c2=64+36  , c2=100 ise   c=√100=10  olur.
|
Â
Sinα=
|
 b
 c  |
Â
=
|
 6
 10 |
Â
=
|
 3
 5 |
|
Â
Cosα=
|
 a
 c  |
Â
=
|
 8
 10 |
Â
=
|
 4
 5 |
|
Â
tanα=
|
 b
 a  |
Â
=
|
 6
 8 |
Â
=
|
 3
 4 |
|
Â
Cotα=
|
 b
 a  |
Â
=
|
 8
 6 |
Â
=
|
 4
 3 |
|
 |
 Önemli özel açıların trigonometrik oranları:
| α |
0 |
30 |
45 |
60 |
90 |
| Sinα |
0 |
1/2 |
√2 /2 |
√3/2 |
1 |
| Cosα |
1 |
√3/2 |
√2 /2 |
1/2 |
0 |
| tanα |
0 |
√3/3 |
1 |
√3 |
Tanımsız |
| Cotα |
Tanımsız |
√3 |
1 |
√3/3 |
0 |
|
 |
|
 Trigonometrik fonksiyonların bölgelere göre açı değerleri:
|
1. BölgedeÂ
Sin(2kπ+α)=Sinα
Cos(2kπ+α)=Cosα
Tan(2kπ+α)=Tanα
Cot(2kπ+α)=Cotα
|
 Örnek:
Sin(420)=Sin(360+60)=Sin60  (1. bölgede sinüs değeri pozitif sayıdır.)
Cos390=Cos(360+30)=Cos30   (1. bölgede cos değeri pozitif sayıdır.)
Tan380=Tan(360+20)=Tan20   (1. bölgede tan değeri pozitif sayıdır.)
Cot750=Cot(2.360+30)=Cot30  (1. bölgede cot değeri pozitif sayıdır.)
|
|
2. BölgedeÂ
Sin(π-α)=Sinα
Cos(π-α)=-Cosα
Tan(π-α)=-Tanα
Cot(π-α)=-Cotα
|
 Örnek:
Sin120=Sin(180-60)=Sin60  (2. bölgede sinüs değeri pozitif sayıdır.)
Cos150=Sin(180-30)=-Cos30  (2. bölgede cos30 değeri - ile çarpılır.)
Tan135=Tan(180-45)=-Tan45 (2. bölgede sin/cos  -  sayıdır.)
Cot120=Cot(180-60)=-Cot60 (2.bölgede cot negatif,  cot60  - ile çarpılır.)
|
|
3. BölgedeÂ
Sin(π+α)=-Sinα
Cos(π+α)=-Cosα
Tan(π+α)=Tanα
Cot(π+α)=Cotα
|
 Örnek:
Sin210=Sin(180+30)=-Sin30  (3. bölgede sinüs değeri negatif sayıdır.)
Cos225=Cos(180+45)=-Cos45   (3. bölgede cos değeri negatif sayıdır.)
 Tan240=Tan(180+60)=Tan60   (3. bölgede tan değeri pozitif sayıdır.)
Cot230=Cot(180+50)=Cot50   (3. bölgede cot değeri pozitif sayıdır.)
|
|
4. BölgedeÂ
Sin(2π-α)=-Sinα
Cos(2π-α)=Cosα
Tan(2π-α)=-Tanα
Cot(2π-α)=-Cotα
|
 |
|
Sin(-α)=-Sinα
Cos(-α)=Cosα
Tan(-α)=-Tanα
Cot(-α)=-Cotα
|
 |
|
 |
| Â |
 |
1)
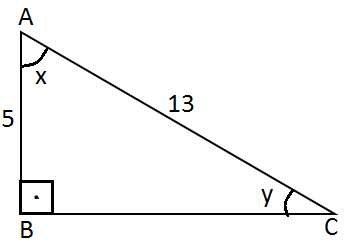
Şekildeki dik üçgende verilenlere göre
Cot x + tan y değeri kaçtır?
|
|
Çözüm :
Pisagor teoreminden , yada 5-12-13 üçgeninden;
|BC| = 12 olur.
Cotx = 5/12 ve tan y= 5/12 olup
5/12 + 5/12 = 10/12 sadeleÅŸirse cevap 5/6 |
| |
|
|
2)
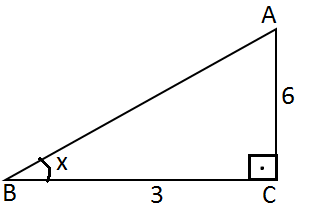
Şekildeki dik üçgende verilenlere göre
Cos x =?
|
|
 Çözüm:
|AB| 2 = 6 2 + 3 2
|AB| 2 = 36 + 9
|AB| 2 = 45
|AB| = √45 = 3 √5
Cos x = 6 / 3 √5
Cos x = 2 / √5
Cos x = 2 √5 / 5
|
| |
|
|
3)
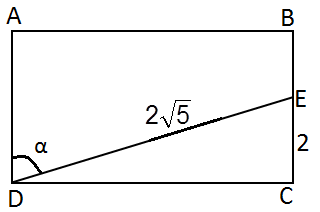
Şekilde verilenlere göre Sin α =?
|
|
Çözüm:
|DC| 2 = ( 2 √5 ) 2 - 2 2
|DC| 2 = 20 - 4
|DC| 2 = 16
|DC| = 4
Ayrıca DEC açısı iç ters açıdan α ya eşittir.
Sin α = Karşı / hipotenüs
Sin α =4 / 2 √5
Sin α =2 / √5
Sin α = 2 √5 / 5
Sin α = 2 √5 / 5 olur. |
| |
|
|
| |
|
|
Gösterim: 58066